Progressões Aritiméticas

----------------------------------------------

Lei dos Senos e Cossenos

LEI DOS COSSENOS

a² = b² + c² – 2bc . cosA

b² = a² + c² – 2ac . cos B

c² = a² + b² – 2ab . cos C

“Num triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois, menos o dobro do produto das medidas desses dois lados pelo cosseno do ângulo oposto ao primeiro lado.”

Exemplo: Quanto vale a?

Resolução:

a² = 5² + 8² – 2 . 5 . 8 . cos 60^º

a² = 25 + 64 – 80 . ½

a² = 89 – 40 = 49

a = 7

Resposta: a = 7

LEI DOS SENOS

a/senA = b/senB = c/senC

“Em todo triângulo, as medidas dos seus lados são proporcionais aos senos dos lados opostos”

Exemplo: No triângulo da figura, calcular a e b :

Resolução:

Resolução:

A = 180^º - 30^º - 45^º = 105^º

Pelo arco soma: sen 105^º = (Ö6 + Ö2)/4

Assim:

6/sen 30^º = a/sen 45^º = b/ sen 105^º

Daí:

a = 6Ö2 e b = 3 (Ö6 + Ö2)

Resposta: a = 6Ö2 e b = 3 (Ö6 + Ö2)

FONTE: http://www.ficharionline.com/ExibeConteudo.php5?idconteudo=5856

----------------------------------------------

Interseção

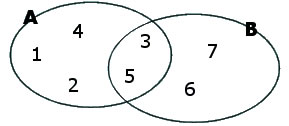
Exemplo de interseção de conjuntos.

Os elementos que fazem parte do conjunto interseção são os elementos comuns aos conjuntos relacionados.

Exemplo 1:
Dados dois conjuntos A = {5,6,9,8} e B = {0,1,2,3,4,5}, se pedimos a interseção deles teremos:
A ∩ B = {5}, dizemos que A “inter” B é igual a 5.

Exemplo 2:
Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7, -8, -9}, se pedirmos a interseção deles teremos:
B ∩ C = { } ou B ∩ C = , então B e C são conjuntos distintos.

Exemplo 3:
Dados os conjuntos D = {1,2,3,4,5} e E = {3,4,5}. A interseção dos conjuntos ficaria assim:
E ∩ D = {3,4,5} ou E ∩ D = E, pode ser concluído também que
E D.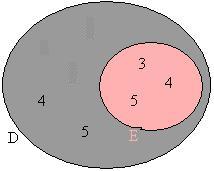



►União
Conjunto união são todos os elementos dos conjuntos relacionados.

Exemplo 1:
Dados os conjuntos A = { x | x é inteiro e -1 <> e B = {1,2,3,4} a união desses dois conjuntos é :
A U B = {0,1,2,3,4}

Exemplo 2:
Dados os conjuntos A = {1,2,3} e B = {1,2,3,4,5} a união desses conjuntos é:
A U B = {1,2,3,4,5}, nesse caso podemos dizer que A U B = B.

►Diferença entre dois conjuntos.

Dados dois conjuntos A e B chama-se conjunto diferença ou diferença entre A e B o conjunto formado pelos elementos de A que não pertencem a B.
O conjunto diferença é representado por A – B.

Exemplo 1:
A = {1,2,3,4,5} e B = {3,4,5,6,7} a diferença dos conjuntos é:
A – B = {1,2}

Exemplo 2:
A = {1,2,3,4,5} e B = {8,9,10} a diferença dos conjuntos é:
A – B = {1,2,3,4,5}

Exemplo 3:
A = {1,2,3} e B = {1,2,3,4,5}a diferença dos conjuntos é:
A – B =

Exemplo 4:
Dados os conjuntos A = {1,2,3,4,5,6} e B = {5,6}, a diferença dos conjuntos é:
A – B = {1,2,3,4}. Como B A podemos escrever em forma de complementar:

A – B = _A B = {1,2,3,4}.

Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola